A colleague asked me a few weeks ago for some advice about their UML class diagram. One of the issues they were having was deciding on whether the link between two of the classes should have a “filled-in” or “non-filled-in” diamond.

You have probably already guessed that he was really asking about whether the two classes were linked by Aggregation (“non-filled-in”) or Composition (“filled-in”). From my experience, this is a very confusing area of UML for some developers. I have reviewed may class diagrams where the developer seems to have just liked the look of one of the diamonds and just used it on all of their associations!

So, where should these notations be used? If you search on the internet you’ll find a plethora of explanations, but I thought it might be useful to try and add a simplified explanation.

First off, this is the difficult part for developers, Aggregation and Composition are nothing to do with code. Both Aggregation and Composition are effectively talking about is one class contains another class. So, many explanations suggest it’s Aggregation if it’s public property and composition if it’s a private field. But unfortunately it doesn’t work like that.

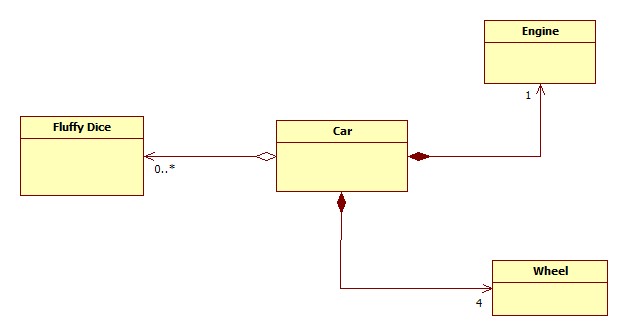
The decision on whether a relationship is a Aggregate or Composite is based on how the classes are related in the real world. Take a classic UML example of a Car class. Your car class may have a engine class, a collection of wheel classes and a fluffy dice class. So, which of these are aggregates and which are composites?

Lets start with the engine class. This is quite a vital part of the car, you couldn’t imagine a car without an engine. Likewise, the wheels are quite important too. In fact you could say that the car is composed of (among other things) an engine and wheels. So, these relationships are examples of Composition.

The remaining fluffy dice class is a bit of a looser relationship. A cars function does not depend on the tacky fluffy dice attached to the mirror. The car may not even have fluffy dice. So, this demonstrates quite nicely a Aggregation relationship.

So, our resulting class diagram looks something like this…